Understanding Polymarket: Why YES + NO Must Equal 1

When discussing Polymarket, many people know that the core principle is: YES + NO = 1. But do you truly understand this simple formula? Today, I'll explain Polymarket's shared order book in depth.

If you check Polymarket's official documentation, you'll find the price calculation explained like this:

The Torn Dollar Bill

Some people think YES at 0.7 + NO at 0.6 = 1.3 should be fine in a free market, right?

This is incorrect. Although it's a free market, YES and NO are not two separate stocks—they are two halves of the same dollar bill torn apart.

Imagine that Polymarket doesn't sell lottery tickets, but rather redemption vouchers for the future.

Each voucher is always worth exactly $1.

The market tears this $1 into two halves: one labeled YES, the other labeled NO.

On settlement day:

• If the event occurs: YES voucher = $1, NO voucher = $0
• If the event doesn't occur: YES voucher = $0, NO voucher = $1

Therefore, at settlement, under the premise of market efficiency with complementary outcomes in the same market and settlement conditions: if you collect both YES + NO, you've essentially bought something that will definitely be worth $1 at expiration.

Multi-Option Markets

Many people might say that some trades aren't just YES and NO—there can be many options.

For example, predicting Bitcoin's price has many price levels, and Elon Musk's tweet count has many quantity options.

If you've used Polymarket's API, you'll find that each option has both YES and NO, making each a standalone trade.

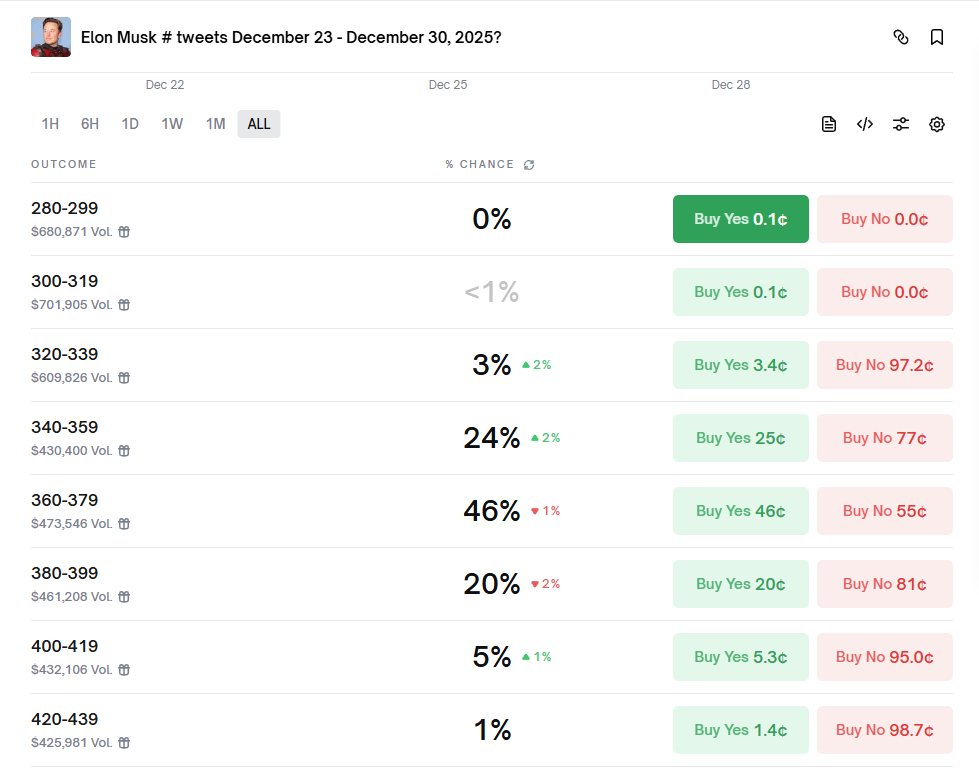
Taking the Musk tweet market as an example, you can see many options. From the API perspective, each title follows the YES + NO = 1 rule.

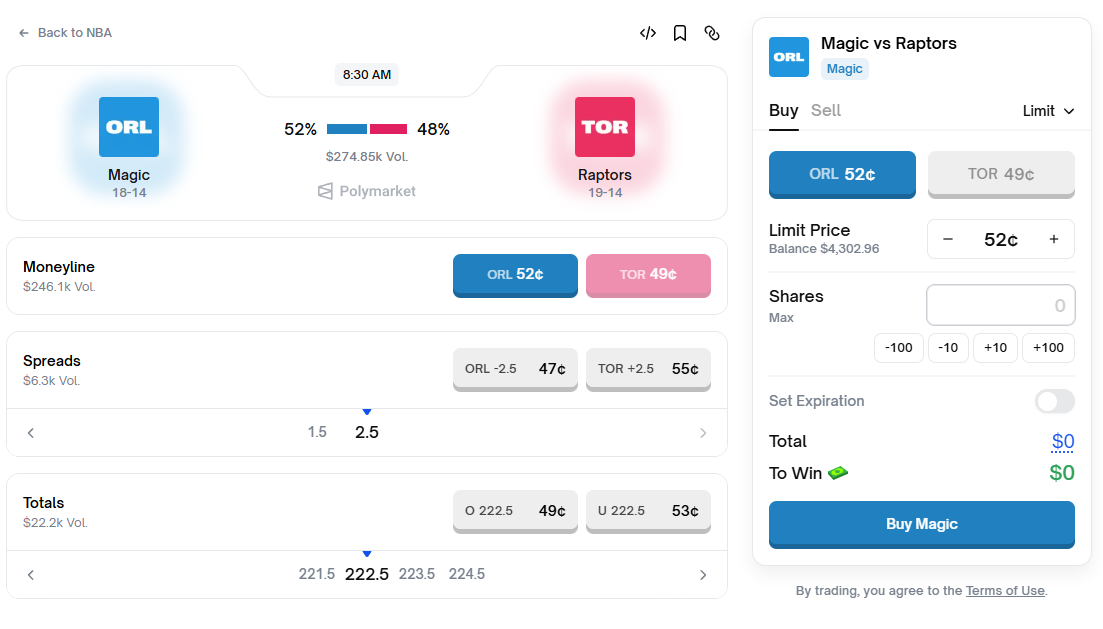
For sports markets like NBA games, you might notice there's no YES and NO—instead, there are team names. In Moneyline betting (predicting which team wins), since NBA games always have a winner (overtime if tied), the home and away teams correspond to YES and NO.

For soccer, draws are possible, so you can bet on home team YES/NO, away team YES/NO, and draw YES/NO.

The Shared Order Book

Many people think Polymarket's order book works like cryptocurrency exchange order books. This is incomplete—the difference is significant because of the YES + NO combination.

Let's return to the official documentation example: "If you place a limit order to buy 'Yes' at $0.60, when someone places an order to buy 'No' at $0.40, your order will be filled. This becomes the initial market price."

How should we understand this? Many people intuitively feel they're trading independently without interacting with others. So why does this matching occur?

This is the magic of the shared order book. Let me demonstrate:

I found a less active market and placed a YES buy order at price 18, quantity 10:

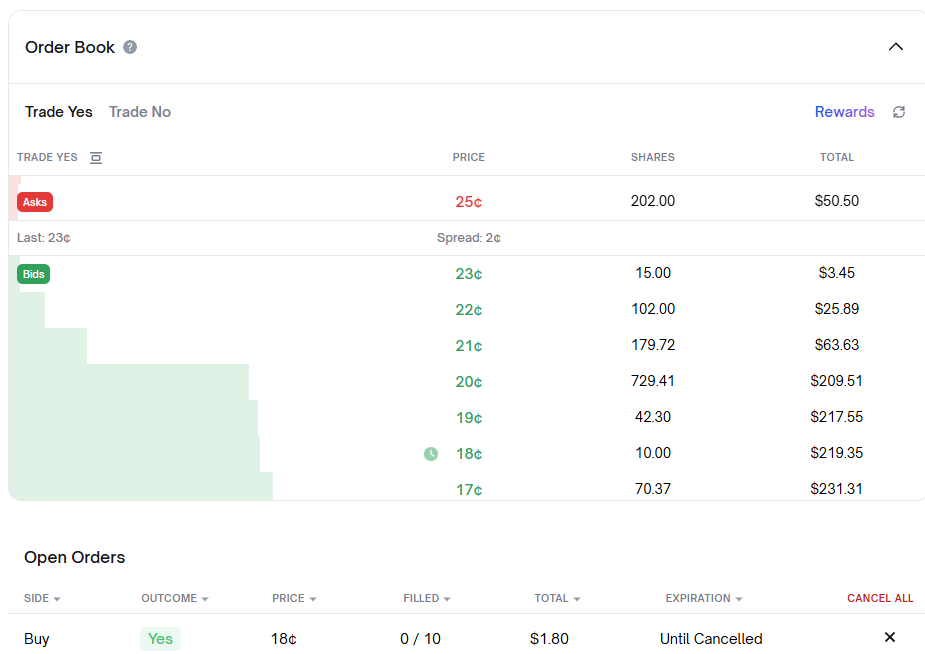
Immediately switching to the NO market:

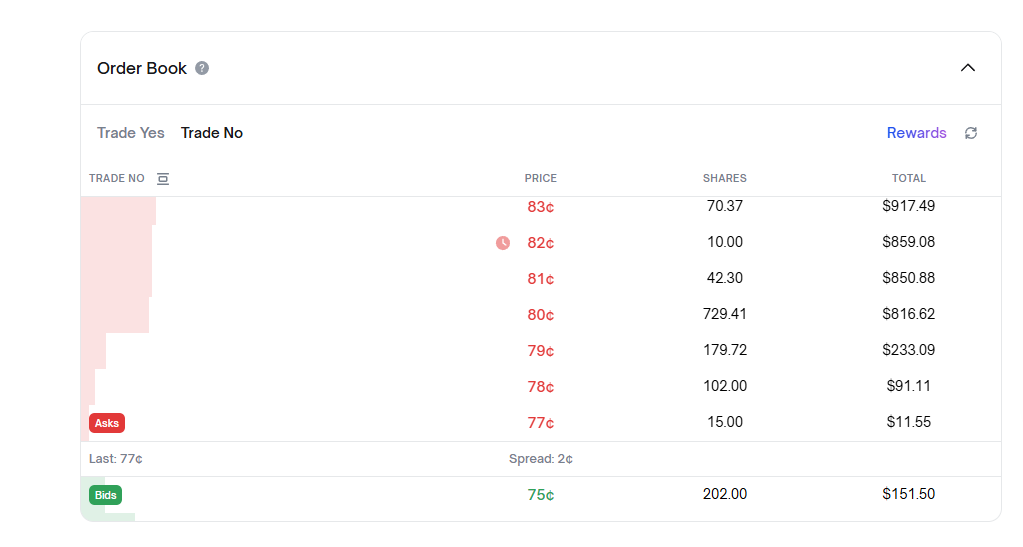
I saw a sell order at price 82 with quantity 10!

Did you notice? The ask and bid on both markets mirror each other!

My buy order at price 18, quantity 10 becomes a sell order at price 100 - 18 = 82, also quantity 10 on the other side!

When you try to sell without holding shares:

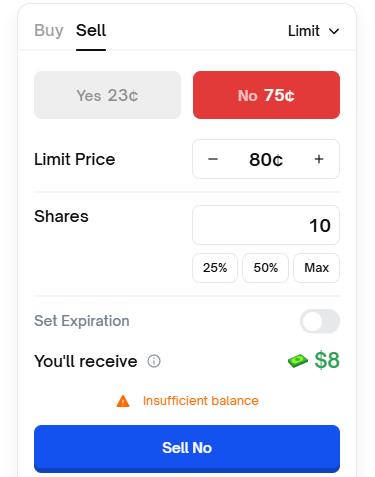
The formula is: YES + NO = 1 (where 18 corresponds to 0.18 and 82 to 0.82—displayed as two digits to represent probability).

Now revisit the official example: "If you place a limit order to buy 'Yes' at $0.60, when someone places an order to buy 'No' at $0.40, your order will be filled."

Using my order as an example: I placed a YES buy order at 18. If someone sells to me, they're actually buying the NO order at 82. After the transaction, I hold YES at 18, they hold NO at 82. Our two vouchers combined satisfy: YES + NO = 1.

Why not just have two independent order books? Why mirror them?

The answer is liquidity! Merging order books concentrates liquidity and improves price discovery efficiency!

The Arbitrage Illusion

Now that you understand YES + NO = 1 and the shared order book, let's examine the arbitrage strategy many KOLs recommend: buying when YES + NO is less than 1 in the same market. Do you think this arbitrage opportunity exists?

The understanding is: YES sells at 0.4, NO sells at 0.4, buy both for 0.8, redeem for $1, profit $0.2!

This strategy is impossible with a shared order book.

When you place a sell order for YES at 0.4, the system interprets it as you wanting to buy NO at 1 - 0.4 = 0.6.

Now, another person wants to sell NO at 0.4.

What happens?

• Your real intent: buy NO at 0.6
• Their real intent: sell NO at 0.4
• Your bid (0.6) is higher than their ask (0.4)!

Result: The system instantly matches you both. No third party ever sees this opportunity.

If you still don't understand, imagine the shared order book as a self-balancing scale following the rule YES + NO = 1.

If you try to break this balance, the system makes you trade directly—others never see the imbalanced orders.

Only orders where YES + NO is greater than 1 remain visible.

Stop dreaming about YES + NO being less than 1 in the same market—this scenario will never appear on your screen!

Correct Arbitrage Methods

Multi-Option Arbitrage

Using mutually exclusive options covering the entire range as an example:

Take the Musk tweet count market with about 30 options from under 20 to 580+, covering the entire range from 0-580+.

If you buy YES on all 30+ options, exactly one will become $1 at settlement while others go to zero.

If your total cost for all options is less than $1, you profit the difference.

Do such opportunities exist? Yes, but bots guard them constantly—manual traders can't find them.

Cross-Event Arbitrage

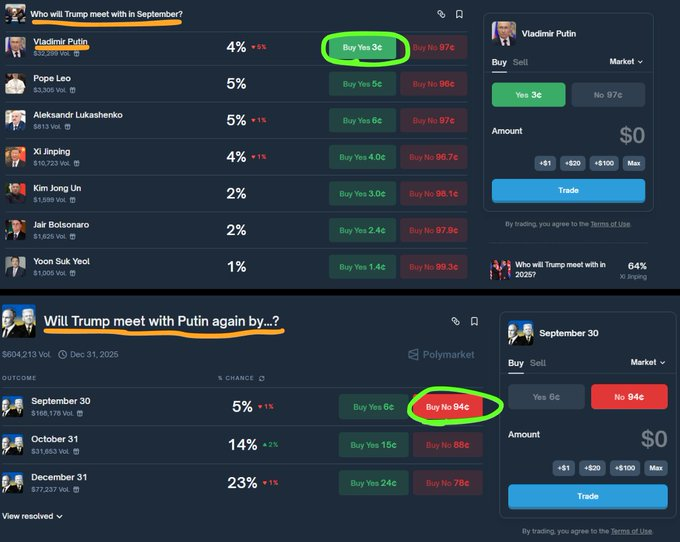
When two events have semantically identical options but different prices, you might find arbitrage opportunities. However, this requires strict judgment and higher technical barriers.

Cross-Platform Arbitrage

The most common is Polymarket to Kalshi arbitrage (Kalshi is US-only; alternatives include Opinion).

If you can buy:

• YES at price = a on Platform A
• NO at price = b on Platform B

And both describe the same event with identical settlement criteria:

Expiration return = $1, Cost = a + b

If a + b + all friction costs is less than 1, it's near-riskless arbitrage.

The hardest part is ensuring "same event"—you must carefully compare settlement rules. Timezone or evidence source differences could turn arbitrage into a nightmare.

Also note the time cost: funds are locked on both sides until settlement unless prices move favorably.

Conclusion

I hope this article helps you truly understand YES + NO = 1. Don't be fooled by KOLs posting strategies claiming YES + NO can be less than 1 for the same event—they might just be using AI-generated content. Even ChatGPT and Gemini don't understand the shared order book unless directed to official documentation.

Understanding this fundamental concept is essential before exploring any trading strategies on Polymarket.